markdown から数式のみを取り出して PNG として出力し該当箇所をパスで置換
なんだか簡単な使い捨てスクリプト程度にしようと思っていたものの, 微妙にしっかり作ってしまったのでその記録.
この記事の執筆時現在, このログのように, gitbook でのビルドが失敗することがある.
発生する条件としては, 文中に大量の数式があり, それを mathjax プラグインによってレンダリングしようとすると起こるようで, 元々の問題源は gitbook が利用する mozilla 発の
nunjucks によるものとされていたようだが, その修正のマージ後も未だ治ってはいない*1.
元からこの問題を認知していれば良かったものの, コンテンツ内に数式が増えてきてから発生したので対応も出来ず, 今さら gitbook からなにか他のものに移行するわけにもいかず, とりあえず応急処置として, 特定のディレクトリツリーを再帰的に検査し, markdown テキストから独自のブロックで囲まれた数式のみを取り込み(このファイルのように```mrと```mrendで囲んでいる), 該当部分を PNG へ出力し, さらに画像のパスに自動で置き換えるようにした. 数式が書き加えられると, 随時それを PNG にしてそのパスで置換するようにしているので, 数式を画像にしたことによって, 作業間で特別な手間を感じずには済んでいるものの, やはり画像の読み込みは重いので, そのうち自前でホストするなど、移行を考えざるをえない状況になっている.
特に gitbook の PDF 出力機能では SVG がサポートされていないために, 出力を PNG 形式で行っている. また, gitbook IO
によるプラグイン, gitbook-mathjax は目次から mathjax によって変換される数式を含んだコンテンツを開くと正常にプラグインが読み込まれず, 結果として再読み込みを行う必要があるなどの問題がある. はっきり言って, 今から数式を多分に含むような文書を gitbook によって管理することは, このような理由から全くもってお勧めできない.
今回の実装では Typescript を利用したわけだが(tumblr クライアントの開発を含めて今回で 2 回目の利用), 今更ながら全体的に関数型言語っぽく書けるリスト処理に少し感動した.
Proof of infinite geometric series
16.8 float のしくみ · ThePolitewaylearntoCPP17 の補足記事。命題「 は
のとき収束し、その値は
である。
のとき発散する」は、高校数学の範囲なので、特別に取り上げる必要はないと思ったが、コンテンツ内容をなるべく自分で書いた文章のみ完結できるよう、本エントリで扱うこととした。といっても、証明はとても簡単に行うことができる。
とする。無限等比級数第
項までの和を
としたとき
が得られる。両辺を
倍すると
が得られる。このとき式
で 式
を引くと
が得られる。
について解くと
となる。また
がいえる(絶対値が
未満である値を掛け続けていくといずれ
になる)。
求める無限級数の値は であるので 式
を利用して
と導出される。
題意は示された。
Divergence of the sum of the reciprocals of the primes
素数の逆数和が発散する事(式 )についてメモ。
素数の逆数和が発散することの証明には Harmonic series*1 が発散する事(式(2))を利用する
式 (2) の証明には、式変形、等式変形による不等式の評価を行う方法と、積分を用いた不等式評価など*2による方法がある。まず式
を証明し、その後式
を証明する。
不等式による (2) の証明
他の発散系列と比較する事で Harmonic series の発散を容易に証明できる。
このとき、
である。式
は次の等式
の通り発散する。
現時点で
の関係性から明白であるが、さらに、この変形を一般化する事ができ、次の不等式が得られる。
式
において
とすると、右辺が発散するため左辺も発散する事が言える。
題意は示された。
積分による (2) の証明
By Jim.belk - Own work, Public Domain, Link
ここで
式
余談
調和級数 は見ての通りゼータ関数
の
に等しく、ゼータ関数は
のときのみ収束する。
(1) の証明
以下の素数を昇順に
とすると次の式が成り立つ。
式
においては、
を
以上の自然数とし、左辺を全て展開すると、
以上
以下のいかなる自然数も
と素因数分解できる。また、同式の右辺を展開すると
が
以上のどのような自然数だとしても必ず
となる項がでてくるため、成り立つことが言えるのである。
次に式 の右辺を等比級数の和の公式で変形すると次の式を得る。
式
は両辺とも正であるため、次のように不等式の対数を取ることができる。
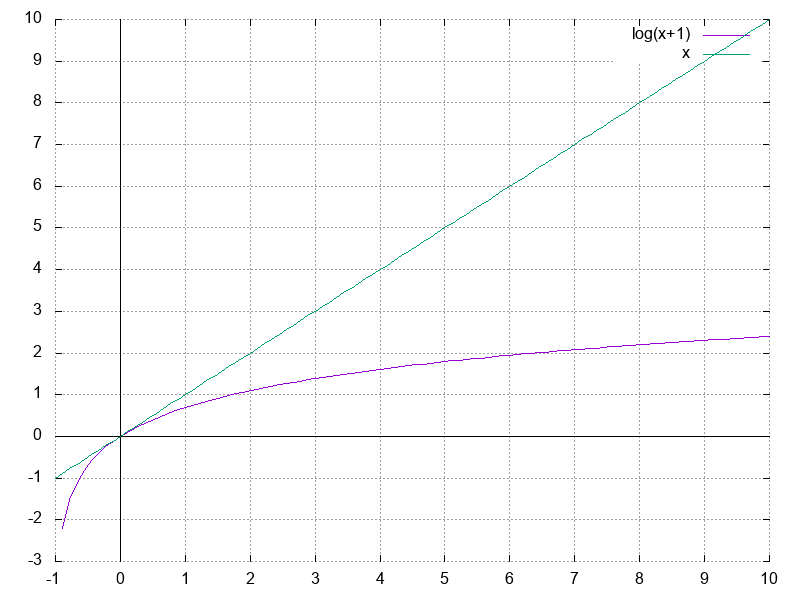
この事実から、式 は次のように変形できる。
ここで、
(
番目の素数より
番目の素数は
以上大きい)であるから式
を変形し次の式を得る。
式
、式
の関係性から、式
は次のように変形できる。
ここで
とすると式
より左辺が発散するため、右辺も発散する。
題意は示された。
総括
最後に素数の逆数和をプロット。

グラフの通り、発散のスピードが非常に遅いことが窺える。素数列の生成などで篩落とす際は、十分に値が増えたとしてももかなり時間計算量を抑えられるであろうことが視覚的に分かる。プロットで用いた値は、自作ライブラリを利用して次のようにして生成した*4。
#include <srook/math/primes/progression/sieve_atkin.hpp> #include <srook/math/constants/algorithm/pow.hpp> #include <srook/math/constants/algorithm/approximate/reciprocal.hpp> #include <srook/string/to_string.hpp> #include <fstream> int main() { constexpr auto max = static_cast<srook::uint32_t>(srook::math::pow(10, 6)); std::ofstream ofs("data.csv"); std::size_t i = 0; float sum = 0.0; srook::math::primes::progression::compute_sieve_atkin_if(max, [&ofs, &i, &sum](srook::uint32_t x) { sum += srook::math::approximate::reciprocal(static_cast<float>(x)); ofs << srook::to_string(i++) + "," + srook::to_string(sum) + "\n"; }, [&ofs, &i, &sum](srook::uint32_t) { ofs << i++ << "," + srook::to_string(sum) + "\n"; }); }
グラフは次のように描いた。
#!/usr/local/bin/gnuplot reset set object 1 rect behind from screen 0,0 to screen 1,1 fc rgb "#333631" fillstyle solid 1.0 set term png size 800, 600 enhanced set output 'image.png' set grid lc rgb "white" lt 2 set border lc rgb "white" set key tc rgb "white" set title tc rgb "white" set xlabel "x" tc rgb "white" font ",30" set ylabel "y" tc rgb "white" font ",30" offset 1, 0 set size ratio 2.0/(1.0 + sqrt(5.0)) set palette rgbformulae 22, 13, -31 set style line 1 lw 2 lt rgb "#008AD4" set xrange [0:] set logscale x set format x "10^{%L}" set format y "%3.1f" set datafile separator "," set title "The sum of the reciprocals of the primes" plot "data.csv" using 1:2 w l ls 1
参考
*1:調和級数。音楽の高調波という概念から派生してこのように名付けられている。
*2:英 Wikipedia Harmonic series には "There are several well-known proofs of the divergence of the harmonic series. A few of them are given below." とある通り、これら以外の証明方法がマクローリン型不等式を用いた方法などを含めて、いくつか存在する。
*4:素数で単に 1 を割れば良いのだが、グラフの様子は大して変わらないので、速度の向上を図るために近似値でプロットしている。言い始めれば、浮動小数点数を使っている時点で近似であるわけだが、106 までの素数の逆数の総和となると図の通り小さい値しか出てこないので、その影響はそこまで酷くもないだろうなどと思いつつ。
zlib ラッパー
少し以前に実装したものの話題となるが、zlib のラッパーを自作ライブラリの方に実装したものの、ブログに特に書いていなかったのでそのメモ。次のように利用できる。
テストは次のように、フリードキュメントである赤毛のアンのテキストを圧縮/解凍をし、それぞれ gzip との実行結果で差異がないかをチェックすることで行なっている。
1 種類のフリードキュメントに対する圧縮, 解凍ではテストが不十分であるように感じたのと, 単一のサーバーに対して負荷がかかってしまうことを避けるために, 候補からランダムでフリードキュメントを選択し, それを利用してテストするようにした.
最後にこれはお遊びであるが、当然 git の blob オブジェクトも同ラッパーで解凍できる(意味はない)。次は普通にgit cat-fileによって blob オブジェクトを解凍/閲覧している例。
$ git clone https://github.com/falgon/git_playground.git $ cd git_playground $ git cat-file -p HEAD | grep tree | sed -e s/tree// | xargs git cat-file -p | cut -d ' ' -f 3 | cut -f1 | xargs git cat-file -p | cut -d ' ' -f 3 | cut -f1 | xargs git cat-file -p hello
似た機能を同ラッパーで次のように実装できる。blob オブジェクトは、コード内のコメントにある通りある一定のフォーマットのヘッダが先頭にあるので、それをスキップする。
次のように実行できる。
$ g++-7 -std=c++1z -Wall -Wextra -pedantic -lz blob_decompress.cpp -o blob_decompress $ git clone https://github.com/falgon/git_playground.git $ cd git_playground $ ../blob_decompress .git/objects/ce/013625030ba8dba906f756967f9e9ca394464a hello
TMP におけるバインドとその利用
私の観測範囲内ではあまり有名で無いようなので発信。バインドとは C++ において Callable を満たすものに対し引数の束縛を行い、束縛済みの新たな Callable オブジェクトを生成する事を広義に言うが、これを TMP で行うにはどうすれば良いか。つまり例えば次のようにするにはどうすれば良いか。
typedef bind<std::is_same, int> type; type::type<int>::value; // == std::is_same<int, int>::value
C++98 から次期標準規格である C++20 の間で、テンプレートテンプレートパラメータを typedef することはできない。
template <template <class...> class F, class... Ts> struct bind { typedef ??? type; };
しかしこれは意外と単純で、次のようにすれば書ける。
template <template <class...> class F, class... Ts> struct bind { template <class... Us> struct type : std::bool_constant<F<Ts..., Us...>::value> {}; };
TMP とは純粋関数型プログラミングであるので、バインドのような機能は役立つ場面が多い。例えば、与えられたポリシーに従う型でグループ化するといった処理には、次のようにして利用するととても実装が楽だ。
これは次のように動作する。
using srook::tmpl::vt::packer; struct X {}; struct Y { Y(const X&); }; static_assert( std::is_same< srook::tmpl::vt::group_by_t<std::is_convertible, packer<int, int, X, Y>>, packer<packer<int, int>, packer<X, Y>> >::value );
この実装で利用されている take_whileD と drop_whileD は、バインドされたメタ関数を受け付けるメタ関数であるが、基本的には haskell のそれと同等である。尚、この group_by も haskell の それと同等である。さらに、ソート等の処理を記述する際には、指定された順序の逆順を表せる機能があると実装が楽であるがこれも同様にしてバインド機能で達成できる。以下はその利用によるクイックソートの実装である。
この実装では、placeholder の機能を利用して引数の入力をコントロールしている。これは、C++ 標準ライブラリに属するstd::bindを意識して作られたメタ機能であり、次の通り同じようにして動作する。
#include <type_traits> #include <srook/tmpl/vt/bind.hpp> template <class T1, class T2, class T3> struct F : std::conjunction<std::is_same<T1, double>, std::is_same<T2, int>, std::is_same<T3, char>> {}; typedef srook::tmpl::vt::bind<F, srook::tmpl::vt::placeholders::_1, int, srook::tmpl::vt::placeholders::_2> bind_type1; static_assert(bind_type1::type<double, char>::value); typedef srook::tmpl::vt::bind<F, srook::tmpl::vt::placeholders::_2, int, srook::tmpl::vt::placeholders::_1> bind_type2; static_assert(bind_type2::type<char, double>::value);
その他にも、リポジトリにて Variadic templates に対する高度なリスト処理が可能なメタ関数、高階関数などをいくつか公開している。
maximal length sequence
M系列に関する学習メモ*1。
import Test.HUnit import System.IO mulcon :: Int -> Int mulcon 0 = 1 mulcon n = (a * mulcon(n - 1) + b) `mod` m where a = 3 b = 0 m = 7 mc :: [Int] -> [Int] mc = map mulcon main :: IO (Counts, Int) main = runTestText (putTextToHandle stderr False) tests where x = mc [0 .. 11] tests = TestList [ "mc test" ~: x ~?= [1, 3, 2, 6, 4, 5, 1, 3, 2, 6, 4, 5] ]
これは線形合同法*2(漸化式 )の単純な実装であるが、結果からも分かるように、周期は
に強く依存するため*3、大きな値
を用いることで長い周期の乱数を得る事ができる。しかしそれに応じて計算処理の膨大化の他、既知の様々な問題*4がある。M系列は
を Bitwise XOR とした時、次の高次線形漸化式で発生する 1 ビット数列を言い、線形合同法の欠点を克服する。
import Test.HUnit import System.IO import Data.Bits p :: Int p = 3 mseq :: Int -> Int mseq 0 = 1 mseq 1 = 0 mseq 2 = mseq 1 mseq n | p > q = (mseq (n - p) `xor` mseq (n - q)) :: Int where q = 1 invmseq :: [Int] -> [Int] invmseq [] = [] invmseq (x:xs) | x >= 0 = mseq x : invmseq xs isUniqueImpl :: [Int] -> [[Int]] -> Bool isUniqueImpl x (y:z) | x == y = False | otherwise = isUniqueImpl x z isUniqueImpl x y = [x] /= y isUnique' :: [[Int]] -> Bool isUnique' [] = True isUnique' [_] = True isUnique' (x:xs) | not (isUniqueImpl x xs) = False | otherwise = isUnique' xs shiftpPattern :: [Int] -> [[Int]] shiftpPattern [] = [] shiftpPattern xs | length xs >= p = take p xs : shiftpPattern (drop 1 xs) | otherwise = [] main :: IO (Counts, Int) main = runTestText (putTextToHandle stderr False) tests where x = invmseq [0 .. 8] shiftp = shiftpPattern x isunique = isUnique' $shiftp tests = TestList [ "mseq" ~: x ~?= [1, 0, 0, 1, 1, 1, 0, 1, 0], "shift pattern" ~: shiftp ~?= [[1, 0, 0], [0, 0, 1], [0, 1, 1], [1, 1, 1], [1, 1, 0], [1, 0, 1], [0, 1, 0]], "unique check" ~: isunique ~?= True ]
shiftpが示しているように、先頭から 1 ビットずつずらした ビットの数列は、それぞれが他の数列と一切異なる数列、つまり
ビットで表現できるビットパターンを網羅している事が分かる。しかしそれは全てではなく、全てのビットパターンが 0 となる数列は発生されない*5。よって、M系列の周期
は
で求まる事が言える。
この時選ばれる と
の値は次の式が既約多項式となるようにして選ばれる。
次にこれまでで用いた
[※ 追記 もっと単純化できた...
-- 追記ここまで]
蛇足
有名なメルセンヌ・ツイスタ(MT)はこのM系列を発展させたものであり、Twisted General Feedback Shift Register(TGFSR) がはじめに発案された。これは、次の漸化式 によって発生する。
は Twister と呼ばれる
の元を要素とする
の行列である。TGFSR はM系列と同様
の最大周期を持つ、すなわちM系列よりも周期が長く、かつ高速な演算となるような
を選択できることから、M系列よりも優れる。MT はこの TGFSR を改良したものであり、次の漸化式
によって発生する。式
による最大周期が
である時、特に MT19937 と呼ばれる*7。